FDPNP5: The operation of neural networks (Part 1)
Preface: I want to initiate a comprehensive series, “Fundamentals of Digital Pathology for Novice Pathologists (FDPNP)”. This endeavor aims to disseminate knowledge about the utilization of computer vision in the realm of modern pathology to pathologists who want to know more about digital pathology.
Introduction
This is a crucial review in the series, aimed at helping pathologists go into the inner workings of computer-vision models. Without diving too much into mathematical details, I try to lay a solid foundation of understanding, starting from the smallest elements, an artificial neuron, to the significant image-processing operations, convolutional and attention-based layers, employed by these artificial neural networks (ANNs).
A Simple View of an ANN
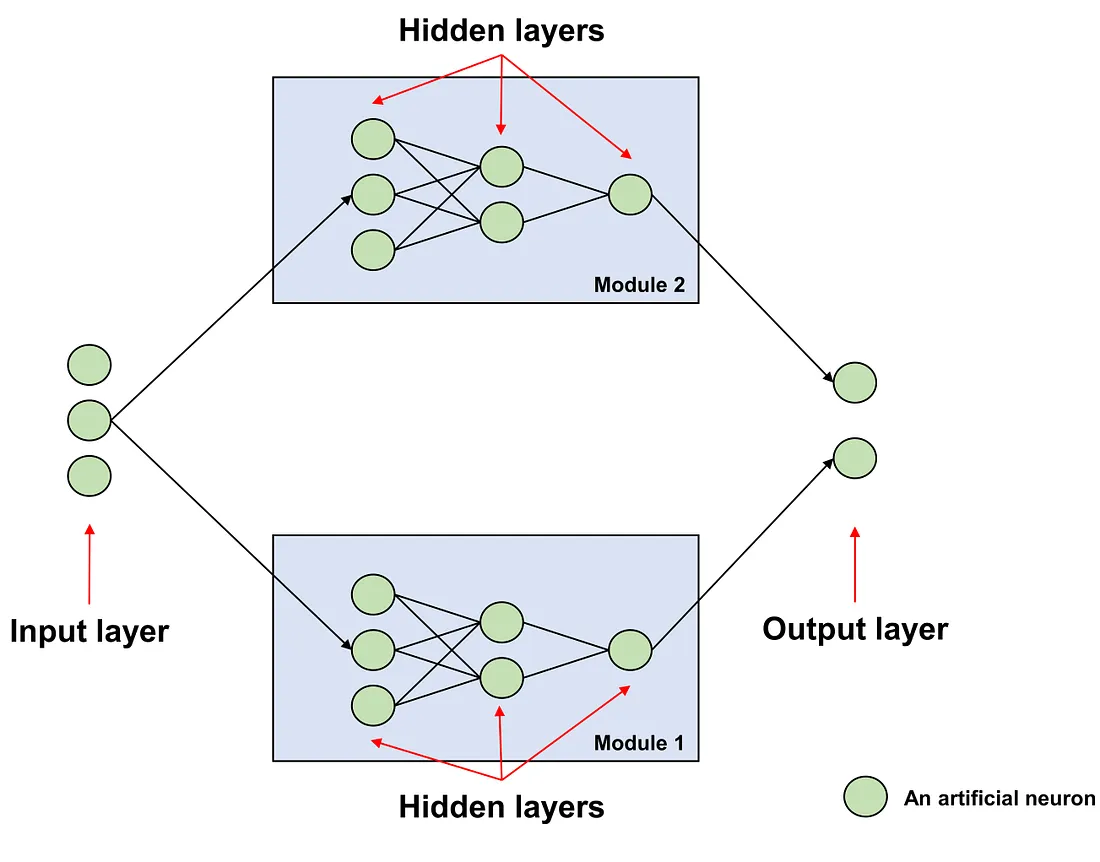
Overview of an ANN - Image by Author
ANN is composed of multiple units known as artificial neurons (ANs). These ANs are typically organized into layers. Each layer of an ANN consists of multiple ANs, which receive input from ANs in the preceding layer or directly from the original features. These ANs then generate output for another set of ANs in the subsequent layer.
The layer that directly receives the input from the original features is referred to as the input layer. The layer that produces the final output, which we interpret as meaningful, is known as the output layer. All the layers situated between the input and output layers are termed hidden layers, primarily because we do not directly interact with or observe these layers.
In an ANN, we often group multiple layers into a functional multi-layered component referred to as a module. A module is a functional construct designed to perform a specific function as intended by its creator.
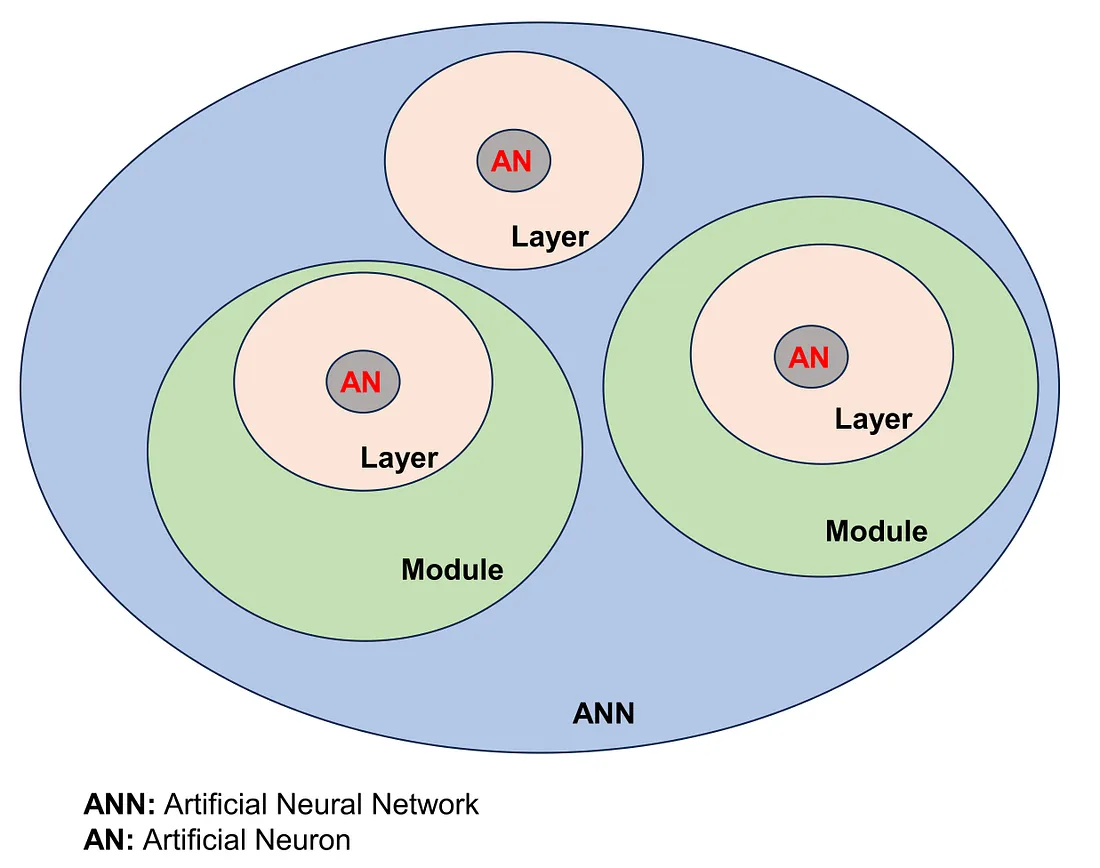
The ANN conponents - Image by Author
Depending on the type of operation performed and the arrangement of the artificial neurons within each layer, we can distinguish between different types of layers or modules. Examples include convolutional layers and modules, attention layers and transformer modules, as well as fully-connected layers and classification modules.
An ANN is composed of numerous ANs. These ANs are typically structured into layers, including the input layer, hidden layers, and output layer. Functionally, many layers can be grouped into a module.
Finally, ANN can be either a non-deep learning model or a deep learning model. Typically, an ANN is considered a deep learning model if it has at least two hidden layers.
A deep-learning model is an ANN with at least 2 hidden layers.
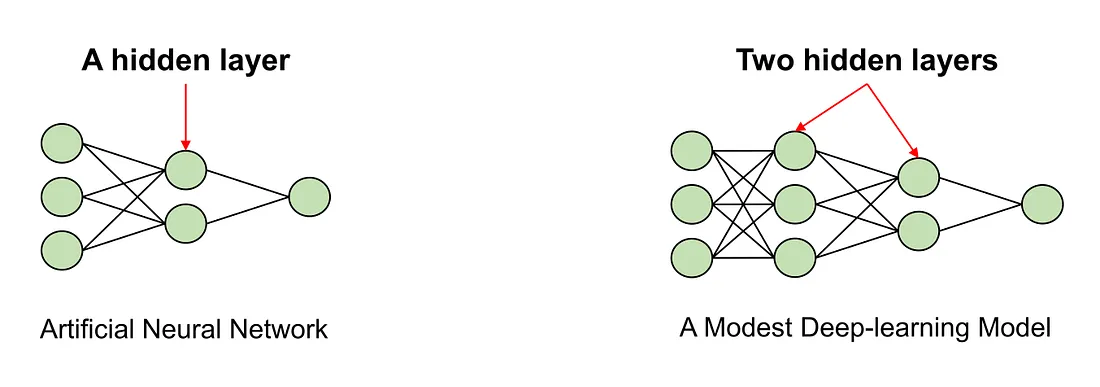
Non-deep-learning and deep-learning models — Image by Author
The Nature of an Artificial Neuron (AN)
Let us examine a single AN. This AN receives a value in and produces a value out.
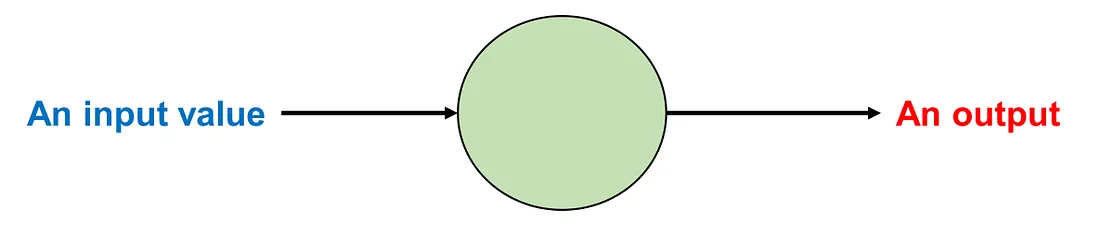
Image by Author
In an AN, we have a “number” by which the input multiplies to yield an intermediate result. This “number” is called a weight. For example, if the input is 3.1 and the weight is 0.2, the resulting weight-input product will be:
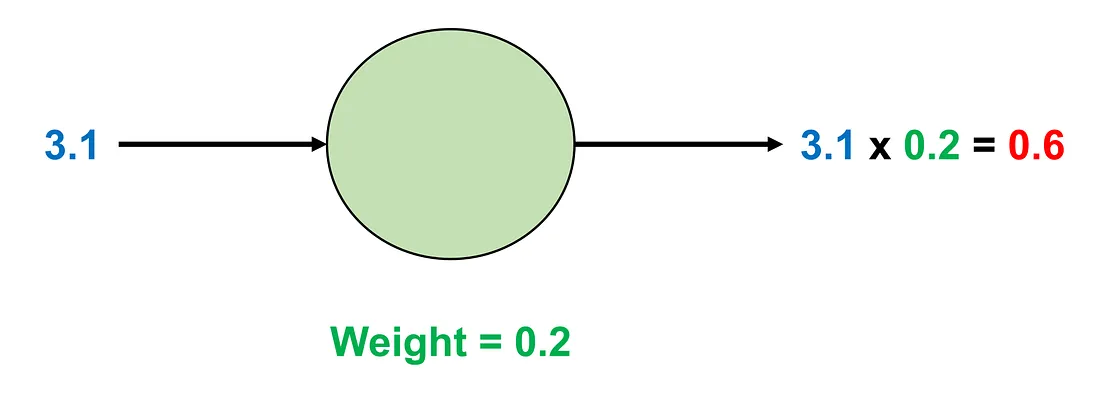
Image by Author
Additionally, an AN usually has another “number” to add to the weight-input product before producing the output. This “number” is called the bias. For instance, if the input is 3.1, the weight is 0.2, and the bias is 0.2, the final result will be:
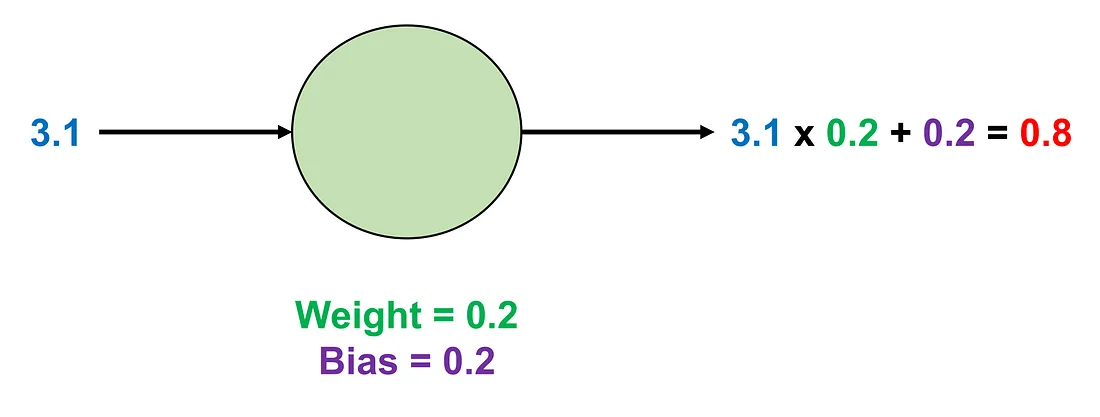
Image by Author
Essentially, weight and bias are called parameters. Another important point is that an AN can have multiple weights but only a bias. For example, we can have an AN with 2 weights in the case of two-dimensional input. If the input has 2 values of (3.1, 2.1), the weights of this AN are (0.2, 0.5), and the bias is 0.2, the final result will be:
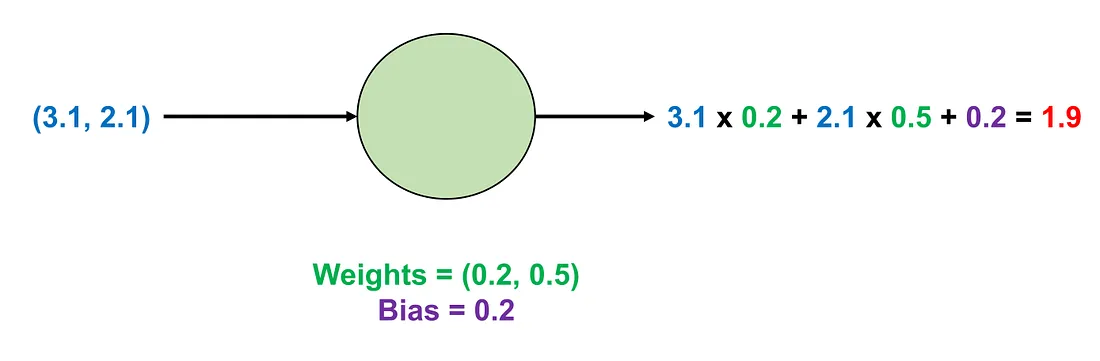
Image by Author
An AN has one or more weights and only a bias. The output value of the AN is weight x input + bias. The weights and bias are called the parameters of the AN.
Finally, an AN only produces an output. However, this output can be sent to more than one AN. For example, if the next layer contains 4 ANs. The only output value of this AN will be sent to these 4 ANs separately.
An AN can have more than one value of input and only a value of output. This output can be sent to many ANs, to which the current is connected, in the next layer.
The Activation Function
Before concluding, let us discuss another crucial component: the activation function. After generating the output of an AN, we often need to modify it before it is processed as input for the next AN. This modification is done using an activation function, which dictates how we transform the output. Common activation functions include the Rectified Linear Unit (ReLU), Softmax, Sigmoid, and Tanh.
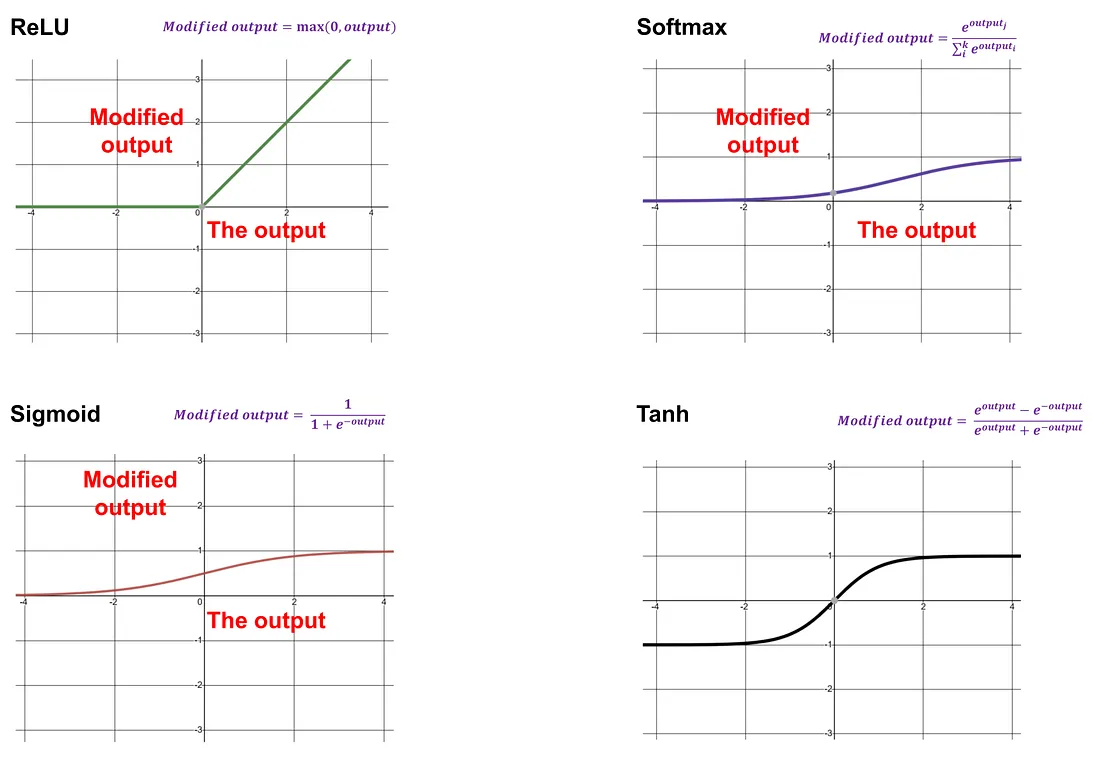
Examples of activation functions — Image by Author
We revisit the previous numerical example. The input is (3.1, 2.1), the weight is (0.2, 0.5), and the bias is 0.2. We have calculated the output as 1.90. Now, suppose we apply the ReLU function to modify the output. Since 1.9>0, the ReLU function will retain the output as 1.9.
If we use the Sigmoid function, the modified output will be the result of applying the Sigmoid function to the original output. The Sigmoid function is given by:
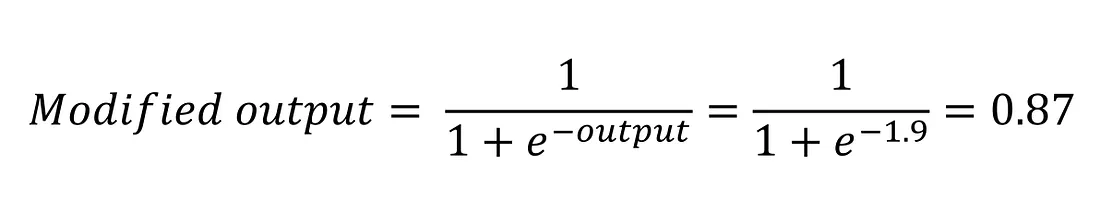
I summarize what we have done so far:
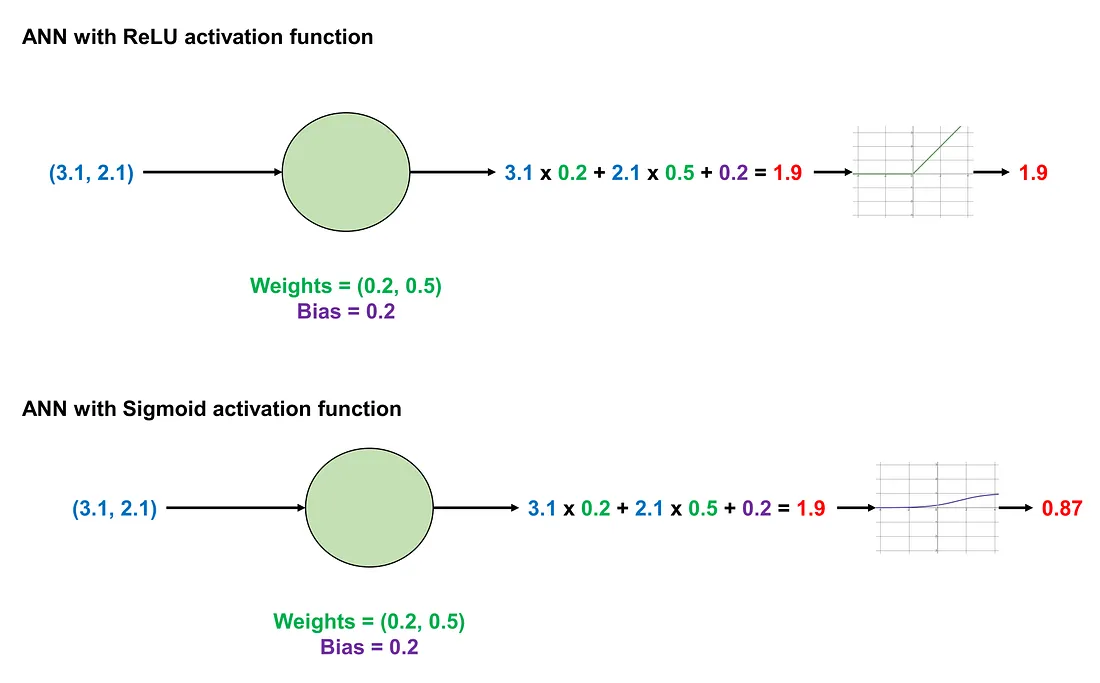
Comparisons of the same ANN using different activation functions — Image by Author
Conclusion
ANN consists of many single units called ANs. An AN contains parameters, called weight and bias, and an activation function. n AN has parameters, called weight and bias, and an activation function. Several ANs form a layer. Depending on the location of the layer, we have an input layer, hidden layers, and an output layer. Layers can be functionally grouped into a module. Finally, an ANN with at least two hidden layers can be considered a deep-learning model.
To those who may be interested, I hope you enjoy this mini-review.