FDPNP1: The Structure of Images
Preface: I want to initiate a comprehensive series, “Fundamentals of Digital Pathology for Novice Pathologists (FDPNP)”. This endeavor aims to disseminate knowledge about the utilization of computer vision in the realm of modern pathology to pathologists who want to know more about digital pathology.
Introduction
The story of digital pathology begins with the understanding of image structure generated by the computer, how the computer “interprets” the image, and whether they perceive the image in the same way we, as humans, do.
Definition of Tensor
We begin our exploration of the image structure in computers by mentioning the definition of a tensor, a mathematical object.
Firstly, we discuss the scalar, which is a single value or number. Examples of scalars include 0.5, -0.2, and 5.2. This is the most basic component of information in an image. We only need one axis to visualize a scalar:
Scalar Visualization - Image by Author
Secondly, we construct a vector from scalars. Consider a pair of scalars (0.5, -0.2); this is known as a two-dimensional vector. We can represent this vector with x=0.5 and y=-0.2. Therefore, any pair of scalars can be considered a two-dimensional vector:
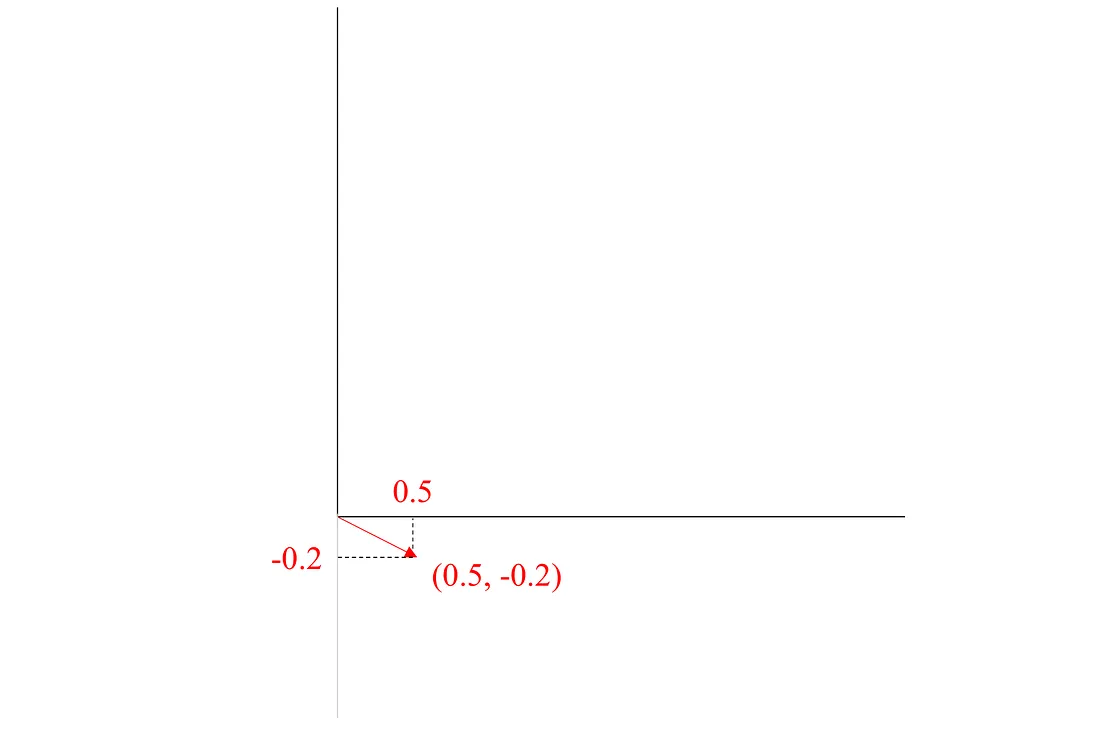Visualization of a two-dimensional vector - Image by Author
Next, we scale up a little more to a three-dimensional vector, which is a triplet of scalars (0.5, -0.2, 5.2). We can represent this vector with three axes: x=0.5, y=-0.2, and z=5.2:
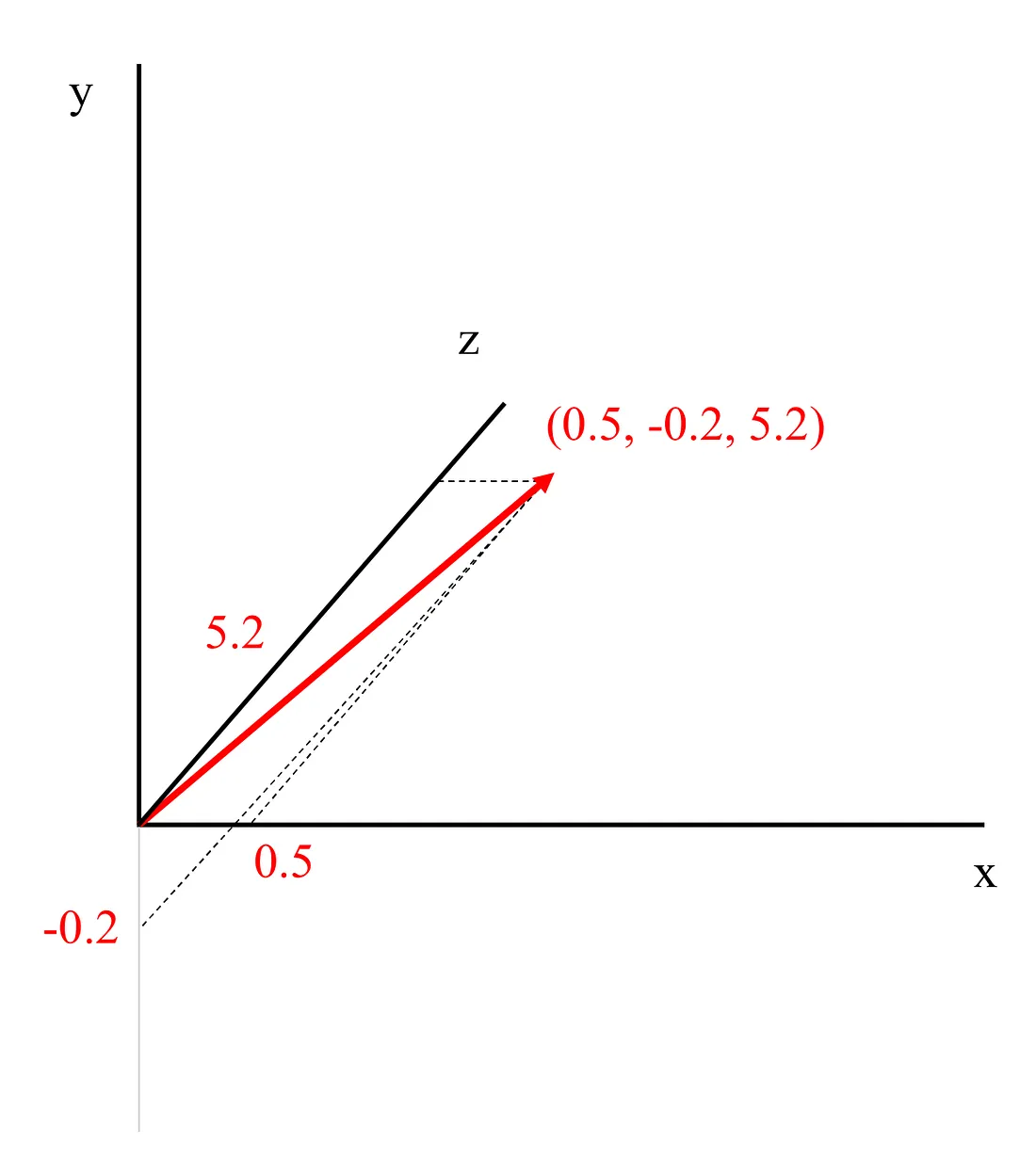Visualization of a three-dimensional vector - Image by Author
We then scale up vectors to form a matrix. Suppose we have a three-dimensional vector v1=(0.5, -0.2, 5.2). We add up four other vectors v2=(1.2, 2.3, 3.4), v3=(3.1, 2.7, 3.6), v4=(1.1, 2.2, 3.3), and v5=(0.0, 2.1, 2.3). We end up with a table (5 rows and 3 columns), where each row represents a vector. This table is known as a matrix:
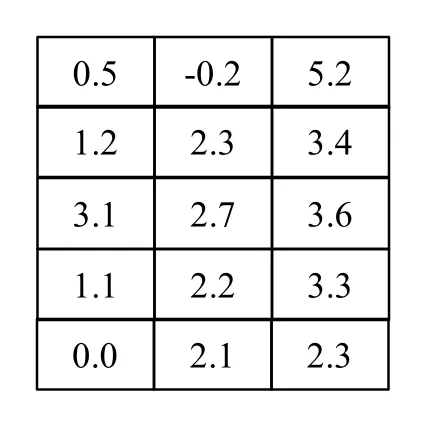A visualization of a 3 x 5 matrix - Image by Author
You might ask, why use a matrix when we could simply use four vectors? The answer depends on the purpose of your observation.
For example, if you want to describe a hand in terms of finger lengths, you would use a 5-dimensional vector. However, if you want to describe a hand in terms of the length of each phalange, you would use a 3 x 5 matrix. Of course, the value for the third phalange of the thumb will be 0 (there is no third phalange in the thumb). Alternatively, you could use three 5-dimensional vectors, but this method of description loses the positional relationship. The first elements in all vectors are related to a finger and are not independent. Similar reasonings are applied to the other 4 elements.
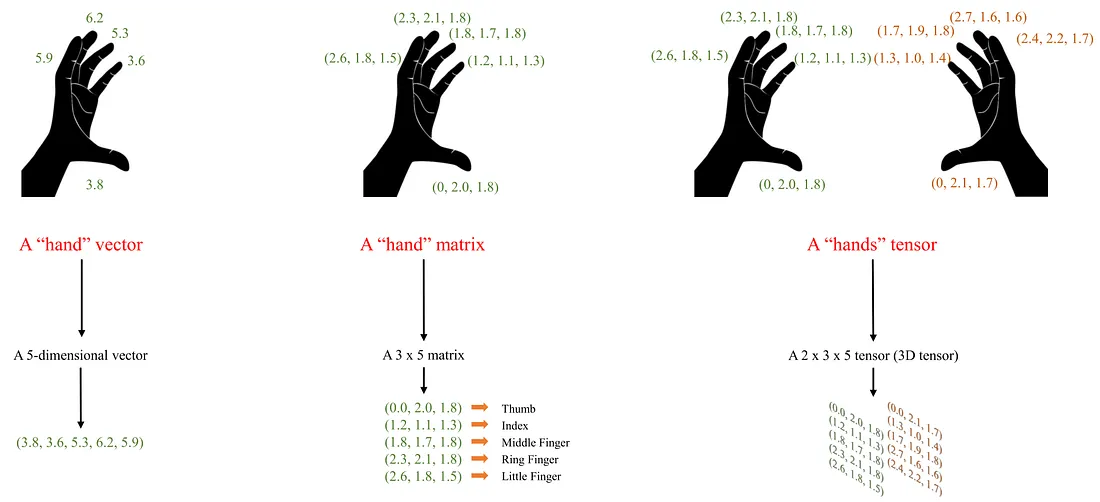Illustrations of the hands under the form of a vector, matrix, and tensor - Image by Author
A matrix is composed of multiple vectors. Fundamentally, it possesses a tabular structure that encapsulates positional relationships. Each row corresponds to a distinct vector, while a column represents a specific element across all vectors.
Using the hand example, describing a person by their hands would require two matrices. Therefore, you would have a mathematical object with 2 x 3 x 5 values. This is called the tensor. You can just describe a person by 3 x 10 values, but you should remember the corresponding fingers on the right and left hands correlate. Therefore, a tensor would make a perfect description where there are 2 matrices, each of which illustrates the phalange length of a hand.
A tensor is a broad term that encompasses both vectors and matrices. A vector, which consists only of rows, is a first-order tensor, while a matrix, with its rows and columns, is a second-order tensor. If we wish to represent multiple matrices for a single object, we require a third-order (3D) tensor, much like the one we used to describe a pair of hands. Following this logic, we might need a fourth-order (4D) tensor to depict numerous 3D tensors for a single object. Similar interpretations can be applied to tensors of higher orders, such as 5D, 6D, and so on, up to n-order tensors.
A tensor is an entity that’s composed of multiple matrices. Essentially, it’s a multi-dimensional structure that encapsulates complex positional relationships. Each slice along a dimension can be viewed as a matrix, and each element within this matrix represents a specific value across all matrices in that slice.
The development of concepts - Image by Author
The term “dimension” in relation to a vector signifies the count of scalar components. This contrasts with the “dimension” of a tensor, which denotes the tensor’s order.
The structure of an image in computer vision
An image is composed of tiny, single-color squares known as pixels. The clarity and sharpness of an image increase with the number of pixels it contains. In other words, a higher pixel count equates to a higher resolution. These pixels form a “matrix” within the image. An image with a resolution of 1024 x 1024 pixels can be visualized as a “matrix” consisting of 1024 rows and 1024 columns of pixels.
An image can be represented by a “matrix” of pixels.
Before delving further into pixels, let us discuss colors. In reality, there is an infinite spectrum of colors. However, this vast array of color shades can be distilled down to just three fundamental colors: red, green, and blue (RGB). By varying the mixing ratios of these three colors, we can reproduce every shade of natural color. By substituting the actual color with three numerical values (or scalars) that represent the RGB ratio, we can readily derive the color from these digits.
Each pixel can be represented by three RGB values.
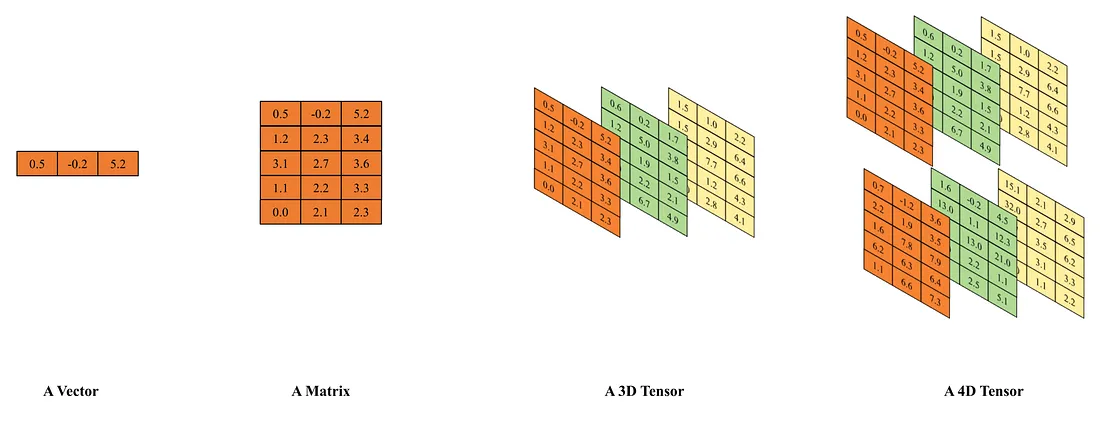
Returning to the topic of pixels, each pixel possesses a single color. Therefore, each pixel can be represented by a color, and in turn, a color can be encoded by three scalars. An image is essentially a “matrix” of pixels, each represented by RGB values. When these elements are combined, they form a tensor. For instance, a 3D tensor of dimensions 3 x 1024 x 1024 represents an image with a resolution of 1024 x 1024 pixels.
Each image can be represented as a 3D tensor - Image by Author
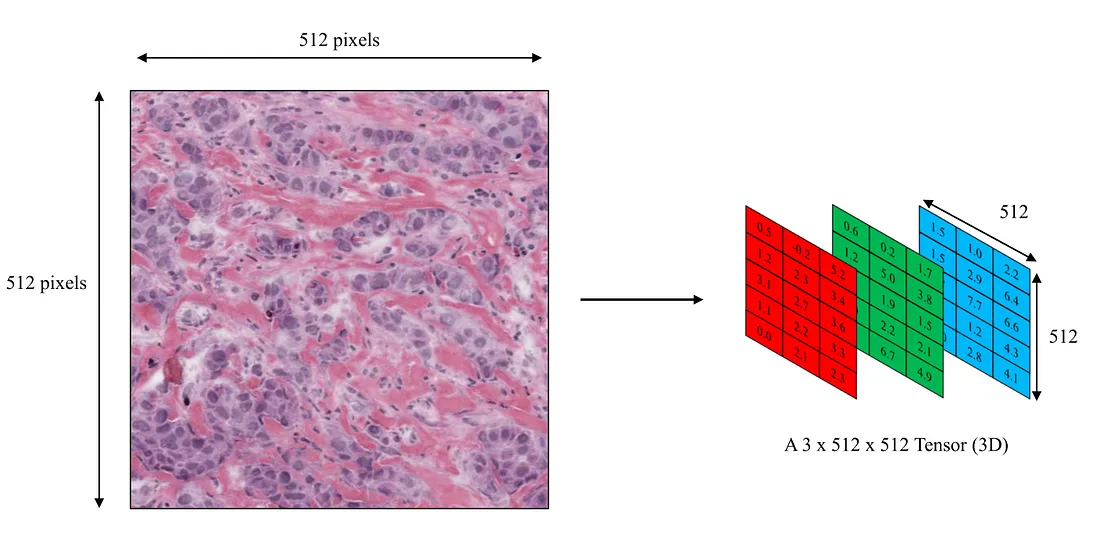
Following this reasoning, an image can be depicted as a 3D tensor, encompassing rows, columns, and the RGB ratio. The RGB values assigned to each pixel are commonly known as color channels. The dimensions of the image tensor are typically denoted as C x H x W, where C stands for channels, H for height, and W for width. A video, that incorporates the dimension of time, can be represented by a fourth-order tensor, expressed as F x C x H x W, where F signifies the number of frames in the video.
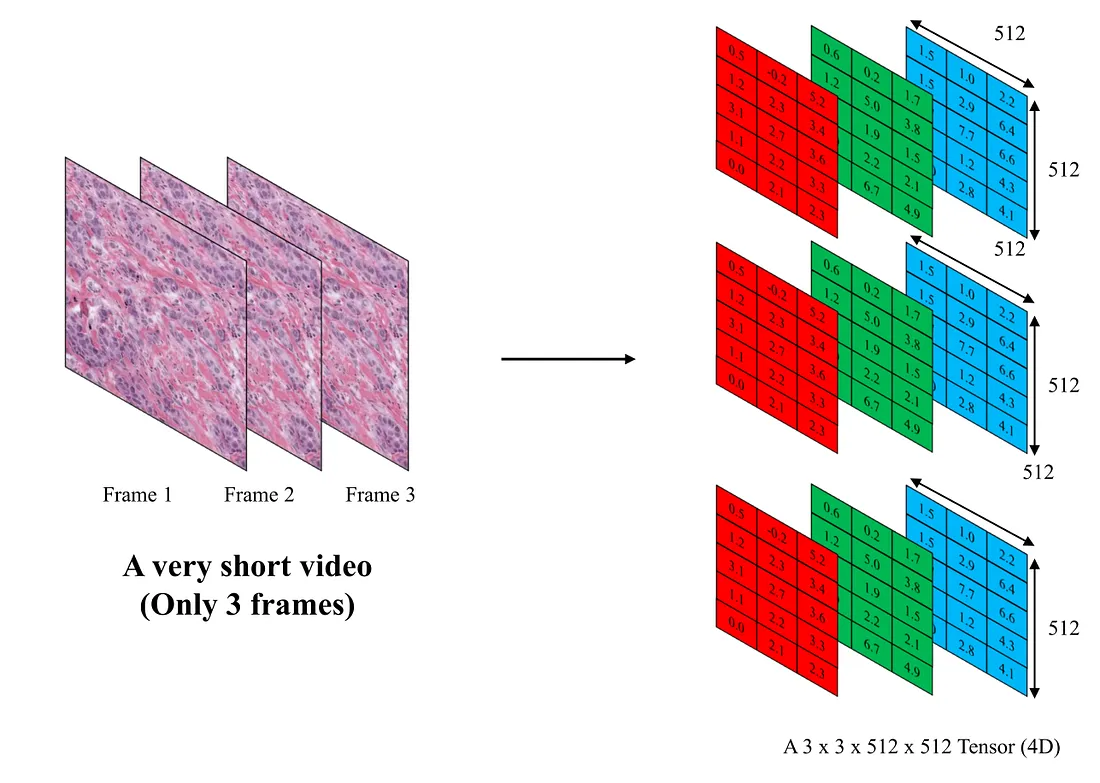Each video can be represented as a 4D tensor - Image by Author
Images and videos are represented by 3D and 4D tensors, respectively.
Conclusion
We as humans interpret images or visual patterns through shapes and colors. In contrast, computers perceive images as 3D tensors and videos as 4D tensors. Computer vision models also process visual data as numerical tensors, implying that there is no “real” image in computer perception.
To those who may be interested, I hope you enjoy this review.